Intersection over union algorithm

Intersection over Union is simply an evaluation metric. Any algorithm that provides predicted bounding boxes as output can be evaluated using IoU. Object detection consists of two sub-tasks: localization, which is determining the location of an object in an image, and classification, which is assigning a class to that object.

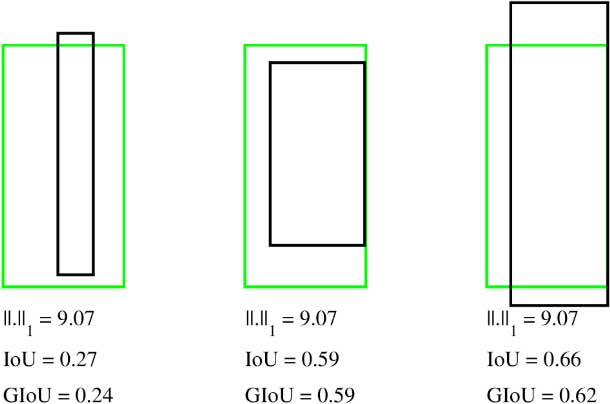
How- ever, there is a gap between optimizing the commonly used distance losses for regressing the parameters of a bounding box and maximizing this metric value. The optimal objec- tive for a metric is the metric itself. The intersection over union computes the size of the intersection and divides it by the size of the union.

When using IoU as an eval- uation metric an accuracy threshold must be chosen. In this paper, we propose an ap- proach for directly optimizing this IoU measure in deep neural networks. The idea is that we want to compare the ratio of the area where the two boxes overlap to the total combined area of the two boxes.

Claude Stolze – A subtyping algorithm for intersection and union types 5. And as we use both for evaluating your object detection algorithm, as well as in the next video, using it to add another component to your object detection algorithm, to make it work even better. In the object detection task, you expected to localize the object as well. In the case of axis-aligned 2D bounding boxes, it can be shown that IoU can be directly used as a regression loss.

Specifically we consider the popular intersection - over - union (IoU)score used in image segmentation benchmarks and show that itin a hard combinatorial decision problem. However, IoU has a plateau making it infeasible to.

To make this problem tractable we propose a statistical approximation to the objective function, as well as an approximate algorithm based on parametric linear programming. We apply the algorithm on three benchmark datasets and obtain improved intersection - over - union scores compared to maximum-posterior-marginal. The standard performance measure that is commonly used for the object category segmentation problem is called intersection - over - union (IoU).

Given an image, the IoU measure gives the similarity between the predicted region and the ground-truth region for an object present in the image, and is defined as the size of the intersection divided by the union of the two regions. The IoU measure can take into account of the class imbalance issue usually present in such a problem setting. A threshold of IoU=0.

Non Max Supression. TO make sure the algorithm detects each object only once. Algorithm traverses edges of polygons until it finds intersection (using orientation test). After intersection it chooses "the most inner" edge from two possible next ones to build intersection core polygon (always convex).

When you have ordered list of vertices, you can calculate polygon area with shoelace formula. Don’t stop learning now.

Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready. Generally, IoU is a measure of the overlap between two bounding boxes. For every event line, it is an easy matter to determine the X intervals spanned by both rectangles, and find their intersection or union.

And the areas between two event lines are trapezoids. Efficient list intersection algorithm. Ask Question Asked years, months ago. Active years, months ago. Viewed 75k times 73. Given two lists (not necessarily sorted), what is the most efficient non-recursive algorithm to find the intersection. Its been a while since I wrote a post. In this post I talk about vectorizing IOU calculation and benchmarking it on platforms like Numpy, and Tensor Flow.

How-ever, there is a gap between optimizing the commonly used distance losses for regressing the parameters of a bounding box and maximizing this metric value. The bounding box coordinates are in the form (x, y, width, height).

In the 3D object detection network, as the depth of the network increases, the size and receptive field of the feature map also change. A lot of blog post already available which are related to the IoU topic. Current post does not pretend to be treasure chest of but here I’ve wrote down couple of notes which helped me understand the algorithm better and implement it by myself.

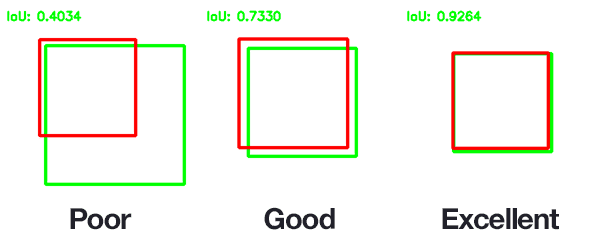
IoU can be visualized as foll ows : Note that, in the preceding picture, the blue box (lower one) is the ground truth and the red box (the upper rectangle) is the region proposal. It is, therefore, the more.

This metric is used in most state of art object detection algorithms. For union (A,B) algorithm, if there are overlaps among geometries of layer A or among geometries of layer B, these are not resolved: you need to do union ( union (A,B)) to resolve all overlaps, i. X) on the produced result X=union(A,B).