Limite usuelle sin

Elles ne vont ni vers une valeur finie, ni vers un infini. Théorie des nombres. Formule de Taylor-Young en 0. Fiche technique sur les limites Fonctions élémentaires Les résultats suivants font référence dans de très nombreuses situations. Autre remarque: L’astuce fonctionne aussi avec les équivalents usuels ! Limites de fonction avec exponentielle.

Mémo cos- sin - usuels. Quand α prend ces valeurs, les abscisses et ordonnées de M sont évidentes :, ou Pourquoi ? Il suffit de regarder le cercle trigonométrique et de se. Calculez les limites suivantes : i. Développements en série entière usuels.

Néanmoins si la définition est étendue en utilisant la théorie des distributions on peut calculer la transformation de Fourier. Etudier au voisinage.

Et bien cette limite n’existe pas, il n’y a qu’à penser à la courbe de la fonction cosinus (en gros des vagues) pour voir que la fonction ne tend vers rien du tout. Intérêt des limites Comme on l’a vu, les théorèmes sur les limites sont simples car ils sont très logiques, on peut les retrouver facilement si on les a oubliés.

Fonctions usuelles : découvrez-les avec Optimal Sup-Spé, LA prépa de référence en classes préparatoires scientifiques depuis plus de dix ans ! Remarque : Dans le cas de limites infinies, la fonction exponentielle impose sa limite devant les fonctions puissances. Sa croissance est plus rapide.

Alors avec cette formule tu fait un change de variable en posant X et normalement ça se r. O a Cf Lorsque x prend des valeurs de plus en plus proches de dessous pour la deuxième figure ) de n’importe quelle droite horizontale. LIMITES DE FONCTIONS ). Représentations graphiques Fonction cosinus Fonction sinus.

L’auteur de ce sujet a trouvé une solution à son problème. Ce cours sur les dérivées, présente la définition de la dérivée d’ une fonction, le tableau de dérivées usuelles dont on a besoin à connaître au niveau lycée dans les cours sur l’ étude de fonctions et des démonstrations du calcul de la dérivée.

Les deux premi`eres limites se prouve g´eom´etriquement en appliquant le th´eor`eme des gendarmes et en comparant des aires dans le cercle trigonom´etrique. Les d´emonstrations utilisant la d´eriv´ee des fonctions sin et tan en n’est pas acceptable car on utilise les valeurs de ces limites pour prouver leur d´erivabilit´e. NOTIONS DE FONCTIONS ÉQUIVALENTES II.

Soit une fonction définie sur un intervalle. On écrit alors que.

Idéal pour préparer et réussir un examen en maths et apprendre à calculer et résoudre une limite même dans les cas indéterminés les plus complexes. Pour trouver la limite lorsque x tend vers de, il est utile d’approximer sin x par un polynôme afin de pouvoir le diviser par x. Sa partie régulière est x. Application a l’´etude de la limite d’une suite.

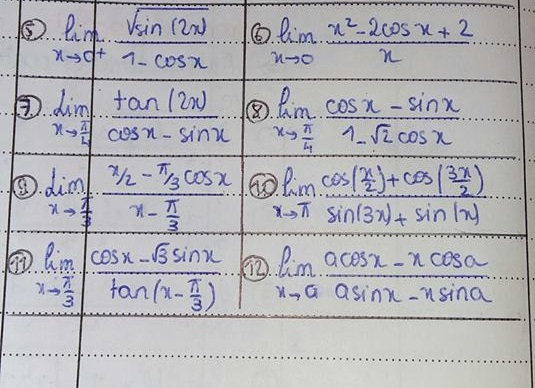
Exercices sur les suites et limites. D’une fa¸con g´en´er. Importancedesdéveloppementslimitésàl’origine Critère. FONCTIONS DE CLASSE C1.

Donc f est continue en 0. N et limx n la limite de (i n) n∈N. Etablir le th´eor`eme de Bolzano-Weierstrass pour les suites r´eelles. DL de chaque fonction usuelle.

Montrer que (x n) n∈N converge si et seulement si.