Arbre binaire de recherche équilibré

Soit E un en-semble. Définition Définition générale. Modèle proposé par G. Adelson-Velsky et E. Alors bande de FDP, vous aimez bien les arbres ? Le code est sur GitHub. Un arbre binaire de recherche (ABR) est une structure de donnée composée de.

Une amélioration consiste à ajouter à. O(log(n)) et en O(1) où n est le nombre de clés représentées dans l’ arbre ). Les arbres binaires de recherche peuvent servir d’implémentation au type abstrait de file de priorité. Pour l’opération de suppression de la plus grande clé, il suffit de. La propriété d’arbre binaire de recherche permet de trouver, d’insérer ou de supprimer facilement un nœud grâce à sa clé en O(h) (figure 1).

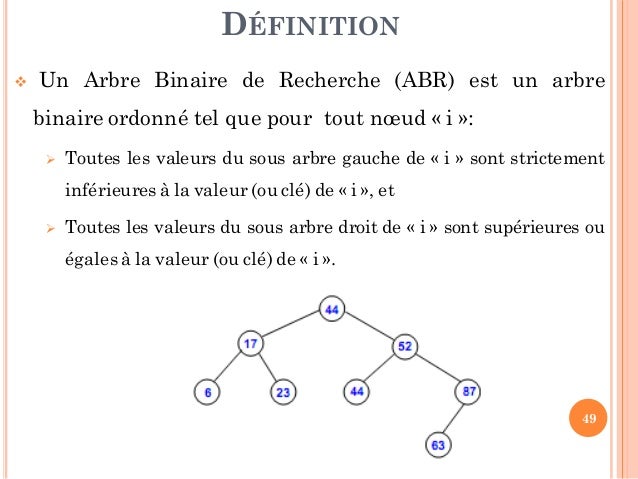
Les fonctions reprennent celles de la définition d’un arbre générique. Autrement dit, A est un arbre binaire de recherche lorsque tout nœud de A est associé à une clé supérieure ou égale à toute clé de son fils gauche, et inférieure ou égale à toute clé de son fils droit.

La règle de rééquilibrage lors de la suppression est également simple. L’objectif de cette réalisa-tion est d’optimiser à la fois l’occupation mémoire et la durée de recherche d’un élément dans un ensemble. Cherchez des exemples de traductions arbre binaire de recherche bien équilibré dans des phrases, écoutez à la prononciation et apprenez la grammaire.

Arbre de recherche équilibré. Dans un arbre binaire équilibré de la taille du problème à résoudre est divisé par deux à chaque itération.

On considère ici des arbres binaires de recherche où les valeurs sont portées par les nœuds internes. Cependant, la réponse que je reçois est plus grande que la hauteur réelle de 1. Soyez le premier à donner votre avis sur cette source. En informatique théorique, les arbres AVL ont été historiquement les premiers arbres binaires de recherche automatiquement équilibrés. Pour se donner une idée, voici un exemple : Un bonzaï binaire de recherche.

Nous allons tâcher maintenant de définir précisément ces fameux arbres binaires. Nous avons vu que pour éviter la dégénérescence de l’ arbre, il existait les arbres binaires H- équilibrés, une autre possibilité est de multiplier les axes de recherche à partir d’un noeud. Dans ce cas, il nous faut utiliser des arbres de recherche.

Ses noeuds peuvent contenirou éléments et toutes ses feuilles sont situées au même niveau. Problème : Après adjonction d’un élément l. Ce que tout le monde semble oublier est que pour les petits N, IE peu de symboles dans votre table, la liste chaînée peut être beauc.

L’objectif de ce problème est l’étude d’une Partie II : Algorithmique et programmation en CaML réalisation particulière de cette structure à base d’ arbres binaires Cette partie doit être traitée par les étudiants qui ont utilisé le langage CaML dans le cadre des enseignements d. On appellera AVL (pour les initiales) tout arbre binaire de recherche équilibré de cette ma-nière. Cet équilibrage fournit une borne logarithme pour la hauteur.

On a donc une excellente complexité sur la classe des AVL. Un arbre de recherche binaire est un arbre binaire structure de données qui fonctionne selon le principe de la recherche binaire. Nous aurons alors deux cas : s’il est inferieur, on fait une recherche dans le fils gauche.

Un arbre B est une généralisation des arbres binaire de recherche dans le sens où il peut avoir un nombre variable de sous- arbres à chaque nœud. De plus un B- arbre grandit à partir de la racine, contrairement à un arbre binaire de recherche qui croît à partir des feuilles. De cette façon, leur recherche est plus efficace que dans un arbre binaire normal et parfois même plus que dans un arbre équilibré. Je vous recommande de commencer avec un arbre rouge-noir ou un arbre AVL.

O(log N) plutôt que O(N) comme la forme dégénérée donne. BSTS Optimal sont généralement divisés en deux types: statiques et dynamiques.

Ce n’est rien de plus qu’un arbre binaire de fouille équilibré.