Limites usuelles pdf

Développements limités usuels Les développements limités ci-dessous sont valables quand x tend vers et uniquement dans ce cas. Formule de Taylor-Young en 0. LIMITES ET CONTINUITÉ (Partie 1) I. Tableau des limites des fonctions usuelles. Fiche méthode : Calcul de limites Comment calculer une limite à l’infini ? Remarque : Dans le cas de limites infinies, la fonction exponentielle impose sa limite devant les fonctions puissances. Sa croissance est plus rapide.

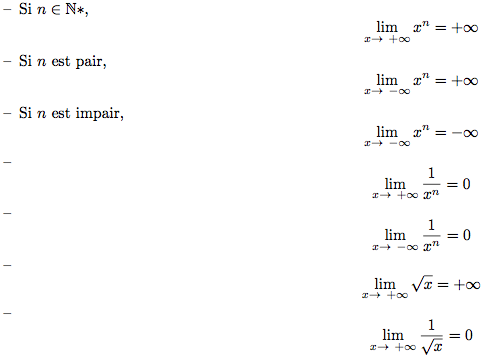
Appliquer les théorèmes des opérations sur les limites, et les limites des fonctions usuelles. Par exemple, les fonctions f(x)=x. Dans cette page, nous allons récapituler ces limites. Théorèmes de comparaison.

Pour conclure, nous rappellerons les limites des fonctions logarithme, exponentielle et puissances. Pour savoir pourquoi il en est ainsi, il suffit de cliquer sur la fonction en question. Définition et notations Définition Notations Soit f une fonction définie sur un intervalle ouvert contenant a. Développements en séries entières usuels Ilyatroisdéveloppementsensériesentièrestrèsimportants(ceuxencadrés),etàpartirdesquelsonpeut. Fonctions de référence.

Ce que vous devez savoir faire Il est important de savoir se ramener à l�. Comparer la limite obtenu avec celle du terme de plus haut degré.

DÉVELOPPEMENTS LIMITÉS 1. Calculer les limites des suites dont le terme général est donné ci-dessous. Etudier au voisinage de z�. Mais ici, seules leurs limites sont intéressantes ! Opérations sur les limites. Dérivation dans le fichier DERIVEE.

Déterminer la limite du a. Limites et Equivalents 1. Les fonctions exponentielle exp : R! Elle peut être un infini ou ne pas exister. Remarque: certaines fonctions n’ont pas de limite à l’infini (voir dessin 6).

Exercice a) Soit f la fonction définie sur R par : f (x) = x. Cours de mathématiques, terminale S: limites de suites Niveau Terminale S Table des matières. En effet la plupart des fonctions usuelles sont continues sur leur domaine de définition. Soit une fonction définie sur un intervalle.

On écrit alors que. Primitives usuelles C désigne une constante arbitraire. Les intervalles sont à préciser. C’est la traduction de la d´erivabilit´e de l’exponentielle en 0. Retrouver quelques limites usuelles Les théorèmes sur les limites concernant les fonctions sont assez proches de ceux rencontrés pour les suites.

Nous n’en donnerons que quelques-uns. Il suffit de se rappeler la r`egle : le signe d’un produit est le produit des signes. Les limites des fonctions usuelles.

Recherche d’un équivalent Intermède : calculer un développement limité.